Tag: computational thinking

Though the concepts and theory behind computational thinking (CT) have been around for decades in the realms of computer science and engineering, it is widely acknowledged that Jeanette Wing’s 2006 publication on computational thinking laid the groundwork for CT’s popularity and integration in 21st century education theory.  Wing (2006) suggested that CT might be considered essential to all human endeavors as it is a distillation of a way that we naturally approach solving problems, managing our daily lives, and communicating and interacting with people.  It need not be relegated only to the STEM fields and computer science majors, because CT is not about getting humans to think like computers.  Rather, CT harnesses the natural outpouring of human cleverness, creativity, and problem solving that laid the foundations for the field of computer science in the first place (Wing, 2006). CT is about “…solving problems, designing systems, and understanding human behavior” by drawing on, and leveraging, the concepts fundamental to computer science (Wing, 2006, p. 33).

Though academics continue to debate an authoritative definition for CT, certain common themes are generally accepted characterizations of CT across the board.  These characteristics include:

• Abstraction — thinking through abstract concepts and ill-defined problems, at times breaking them into smaller, digestible pieces, in order to move towards a more concrete, real-world solution (Wing, 2006).
• Pattern Recognition —  recognizing useful patterns in data, filtering out the characteristics of patterns that aren’t needed, focusing on those that are (Wing, 2006).
• Algorithmic Thinking — curating a list of steps that can be followed to solve a problem (Lyon & Magana, 2020).
• Creative Problem Solving — developing a unique, context-based solution that is  considered original, valuable, and useful (Romero et.al., 2017).
• Evaluating Solutions — considering the efficacy of a proposed solution to a problem, perhaps making considerations for factors like efficiency and resource consumption (Lyon & Magana, 2020).

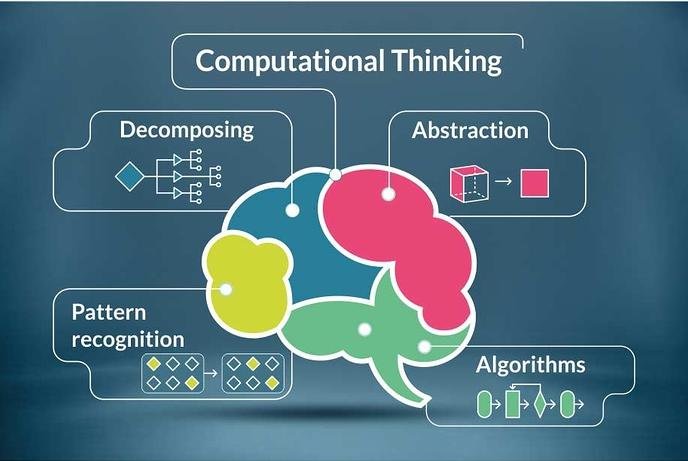
These facets of CT and the related skills are all integral parts of a 21st century education at all levels, including K-12 and postsecondary.  Indeed, “…computational sciences have been deemed essential to maintaining national competitiveness in the workplace and national security.” (Lyon & Magana, 2020, p. 1174)  For these reasons, the fundamentals of CT have been championed in education theory over the last decade, and nationally recognized standards like the Common Core State Standards and ISTE Standards for Students have pointedly emphasized the importance of “21st century skills” in K-12 education while simultaneously offering some clear guidance for what CT can look like in action. 

But what about higher education?  The implementation of CT in higher education classrooms is noticeably harder to call out, especially outside of computer science and engineering classrooms.  In my opinion, this is likely due to a number of factors including, but not limited to:

1. Lack of collegial collaboration:  higher education disciplines are notoriously siloed. Meaningful integration of CT concepts outside of computer science and engineering programs demands intentional professional development for faculty, as well as interdisciplinary cooperation, both of which can be less accessible in higher education.
2. Lack of resources: there is relatively little literature available which provides ideas for practical application of CT outside of computer science programs (i.e. coding and computer programming) at the postsecondary level. Additionally, published standards often lean more heavily towards K-12 education.
3. Questions of applicability: the humanities often resist algorithmic ways of knowing because there is so much value placed on interpretation, subjectivity, and open debate about meaning (Czerkawski & Lyman, 2015).
4. Just getting started: there is growing interest in translating CT pedagogy into a wide variety of disciplines in higher education (and K-12 for that matter), but the research and discussions are just getting started.  There is much yet to be explored.

Knowing that many STEM instructors in higher education automatically incorporate CT in their approach to teaching and learning because of the nature of their field, and knowing that engaging with CT in courses devoted to coding and programming are already integral to computer science and engineering majors, I seek to offer a few alternative examples of CT as it has been used to enhance teaching in learning in other kinds of higher education environments:

• In a professional writing course taught at the undergraduate level, CT was used to systemize the writing process.  It called for a “deconstructive approach, breaking down the task of structured authoring into multiple layers of abstraction, and teaching each layer independently.” (Lyon & Magana, 2020, p. 1182)
• In the fine arts, CT can be used as a tool to enhance creativity.  In one example, CT was used to create an organized system for tracing the origins of musical composers, which in turn inspired new creative endeavors based on the organized data. “…Algorithmic composition in music is, effectively, a human-computer collaboration–the computer serving as a tool that extends the composer’s ability to explore new musical ideas” (Edwards, 2011, p. 67)
• The Stanford Literary Lab famously applied CT via Graph Theory to perform a “network analysis of character relationships and interactions” in a series of Shakespeare’s plays (Czerkawski & Lyman, 2015).
• In the life sciences, CT has been used to inform systems theory and how to teach and understand biological processes, such as genetics, in an organized, logical fashion (Czerkawski & Lyman, 2015).
• Utilizing a process dubbed “creative programming,” instructors may engage learners in the process of designing and developing an original work through coding. In this collaborative approach, learners are encouraged to co-construct knowledge in an interdisciplinary way. Examples might be to have students in a history course (co-)create a rendering of a city at a given historical period, or to present a traditional story in a visual programming tool like Scratch. In this kind of activity, learners must use skills and knowledge in mathematics, technology, language arts, and social sciences. (Romero et. al, 2017, para. 3)

Modeling and simulation activities are excellent examples of CT at work, and these types of learning activities can certainly extend themselves to many types of fields and disciplines.  Consider a learning activity where a group of undergraduate philosophy majors create a simulated narrative presentation wherein a human “character” makes a series of daily choices based on their moral philosophy or framework–almost like a “Choose Your Own Adventure” novel meets systems theory within one, or multiple, philosophical frameworks.  The simulation itself could be a computer-based product (or not), but regardless, the learning activity would draw upon many tenets of CT while also demonstrating in-depth knowledge of the discipline-specific subject matter.

All fields and disciplines require problem solving in some form.  Thus, it is reasonable to assume that CT may be useful in expanding the human ability to effectively problem solve in all fields.  In one study comparing the use of CT by an undergraduate computer science student and an art student, the researchers found that both students “…used various CT skills when solving all [italics added] problems, and the application of CT skills was influenced by their background, experiences, and goals.” (Febrian et. al., 2018, para. 1)  Regardless of training, background, or chosen major, CT enables postsecondary students to become more efficient problem solvers in all areas of life, teaching them to recognize computable problems and approach the problem-solving process as skillfully as possible (Czerkawski & Lyman, 2015).

References

Czerkawski, B.C. & Lyman, E.W. (2015). Exploring issues about computational thinking in higher education. TechTrends 59(2), 57–65. https://doi.org/10.1007/s11528-015-0840-3 

Edwards, M. (2011). Algorithmic composition: Computational thinking in music. Communications of the ACM, 54(7), 58-67. doi:10.1145/1965724.1965742  

Febrian, A., Lawanto, O., Peterson-Rucker, K., Melvin, A., & Guymon, S. E. (2018). Does everyone use computational thinking?: A case study of art and computer science majors. Proceedings of the ASEE Annual Conference & Exposition, 1–16.

Lyon, J. & Magana, A. (2020). Computational thinking in higher education: A review of the literature. Computer Applications in Engineering Education 28(5), 1174-1189. https://doi.org/10.1002/cae.22295

Romero, M., Lepage, A., & Lille, B. (2017). Computational thinking development through creative programming in higher education. International Journal of Educational Technology in Higher Education 14(42). https://educationaltechnologyjournal.springeropen.com/articles/10.1186/s41239-017-0080-z

Wing, J. (2006). Viewpoint: Computational thinking. Communications of the Association for Computing Machinery (49)3, 33-35. https://dl.acm.org/doi/fullHtml/10.1145/1118178.1118215?casa_token=DY3JiA-SOKMAAAAA:OYN4CIuf3LvuR1v4IiYsKQ-2J1KQMV6e0k6skWtib9uI02IKHhX9fEEA7rQC459Lk39QGworokaU